Quasiparticle fragmentation at finite temperature

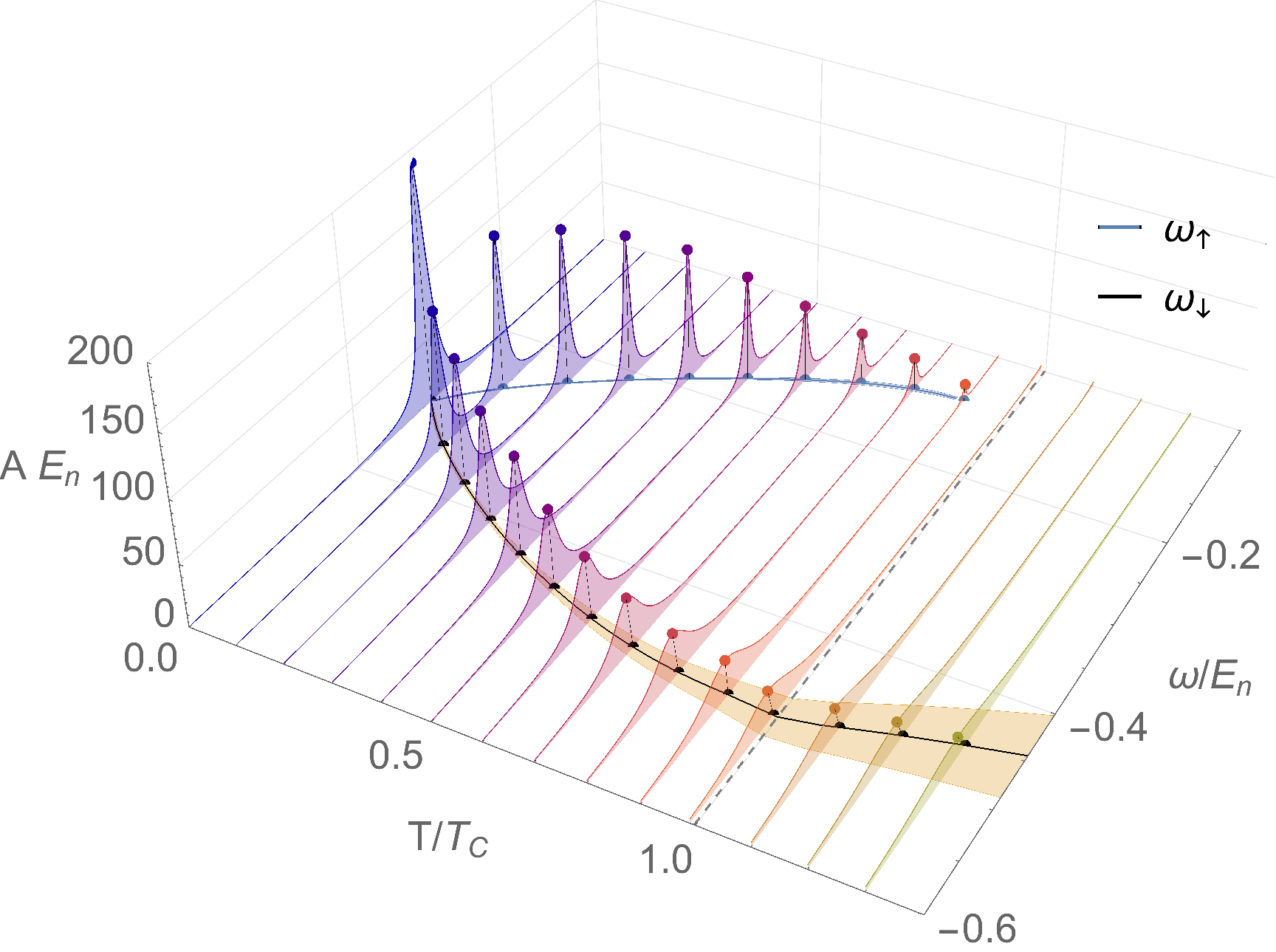
Dilute impurities in a quantum bath constitute a paradigmatic realization of the powerful concept of quasiparticles. Landau, with great insight, argued that the complicated microscopic bath-impurity interactions may be absorbed in a few parameters, and all one is left with are "dressed impurities", the "polarons", which to first approximation propagate as free particles with renormalized properties, like a different mass. While impurities in a Fermi gas are well understood by now, theoretically and experimentally, we show here that impurities in a Bose gas hold an unexpected surprise. Indeed, the quasiparticle describing a single impurity at negative energies at zero temperature fragments into two quasiparticles as soon as the gas is heated up. This is a purely non-perturbative effect due to the coupling of the quasiparticle to a gapless bosonic mode, and it bears strong similarities with a scenario predicted more than 30 years ago (and not yet observed) in a completely different context, i.e., the emergence of "plasminos" in hot quark-gluon plasmas, and in Yukawa and QED theories. Our results show that such intriguing emergent particles can be investigated in the controlled environment of an ultracold quantum gas.

Vortices that won't stand still

The Onsager-Feynman condition says that the integral of the flow velocity along any closed loop inside a superfluid must take discrete values. A famous consequence of this is the quantization of vortices in superfluids. In this paper we describe how the same condition also forces such vortices to move, depending on the macroscopic shape of the superfluid. We investigate the flow pattern of a two dimensional superfluid on a cylindrical surface with one vortex. We find that only a quantized vortex motion of the vortex core with positive or negative sense around the cylinder fulfills the Onsager-Feynman condition. This is a beautiful example of the quantum nature of the superfluid. It hints at the rich physics to be found in the interplay of the topology of a superfluid and vortex dynamics, and provides a direct hydrodynamic analogue of Laughlin pumping. By a conformal mapping, we analyze the related dynamics on the surface of a planar annulus, which is topologically equivalent to a cylinder and which may be more accessible experimentally.